Emotions
The project
The spontaneous formation of regular spatial patterns in complex systems is an outstanding feature of many systems found in Nature. This project aims to contribute to understanding the emergence of such motifs in complex or random systems whose microscopic rules are described by simple rules yet resulting in rich mathematical models. A key aspect of our proposal is characterizing the emerging motifs’ geometric shapes and their fluctuations. We intend to tackle these themes by combining our expertise in the fields of statistical mechanics, integrability, complex networks and dynamical systems, reinforcing thus the burgeoning collaboration between the UNamur Institute for complex systems (naXys) and the UCLouvain Institute for Research in Mathematics and Physics (IRMP) and setting it into a solid and durable ground. By using analytical and numerical methods, we intend to pursue three research axes.
The artic curve phenomenon
The first research axis addresses the so-called arctic curve phenomenon in random tiling and vertex models of planar statistical mechanics. The phenomenon refers to the emergence of deterministic patterns known as arctic curves in a particular scaling limit of these models. The curves spatially separate the models’ solid, liquid, or even gaseous phases. Finding and characterizing these arctic curves, in particular by exploiting integrability properties, is an active research field with yet a great deal of open problems. We intend to contribute to it by investigating so-called surface-on-surface models or higher-spin vertex models, for which characterizations of the arctic phenomenon remain to be found, benefiting from both the analytical expertise of the UCLouvain team and the numerical know-how of the UNamur team.
The universality of fluctuations in the vicinity of arctic curves
The second research axis focuses on the universality of the fluctuations in the vicinity of arctic curves. Universality refers to the appearance of identical features in totally unrelated problems or models. A paradigmatic example is the characterization of the fluctuations around arctic curves in some tiling models by the celebrated Tracy-Widom distribution, which governs the (unrelated) statistics of the largest eigenvalue of certain random matrices. Such observations hint at deep properties of the fluctuations in arctic phenomena, which we intend to investigate.
Random walks in complex networks
The third research axis concerns patterns and universality related to random walks in complex networks. A focus will be the study of the so-called loop-erased random walks resulting from a chronological loop erasure applied to simple random walks. Loop-erased random walks have been thoroughly investigated in regular structures and are connected to a host of models of statistical mechanics, such as spanning trees or the Abelian sandpiles, and continuum theories, for example the Schramm-Loewner evolutions. Combining our knowledge and previous work in these fields with the UNamur team’s expertise in complex network theory, we plan to address the generalizations of loop-erased random walks to complex networks and several simultaneous random walkers.
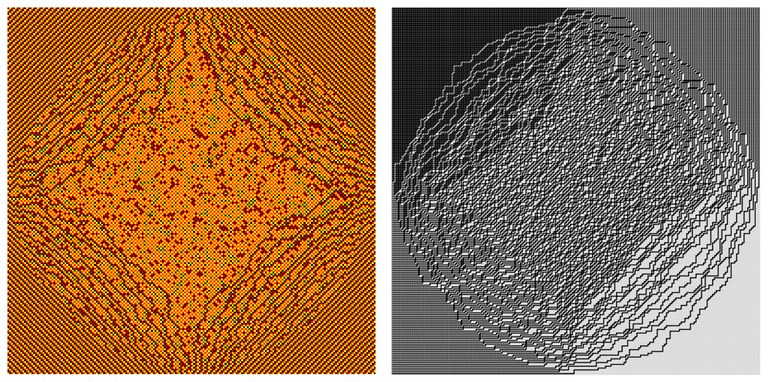
Illustration of spatial phase separation in the three-color model on a square with domain-wall boundary conditions via the sample and its path representation.
The research team
PI (spokesperson) |
Co-PI |
Co-PI |
 |
 |
 |
|
Prof. Timoteo CARLETTI University of Namur (UNamur) Namur Institute for Complex Systems, naXys |
Prof. Christian HAGENDORF Université catholique de Louvain (UCLouvain) Institut de recherche en mathématique et physique, IRMP |
Prof. Philippe RUELLE Université catholique de Louvain (UCLouvain) Institut de recherche en mathématique et physique, IRMP |
More info about the team...
Open PhD position
We are inviting applications for PhD positions in our teams at the UNamur Institute for Complex Systems (naXys) and Institute for Research in Mathematics and Physics (IRMP) at UCLouvain.
The successful candidates will have the opportunity to work within the ARC project EMOTIONS, focussing on topics at the intersection of statistical mechanics, integrable systems, complex networks, and dynamical systems (see project description [insert link here]). The research will be carried out in a dynamic and collaborative environment.
Applicants should hold a Master’s degree in physics or mathematics by the starting date of the position. A strong background in statistical mechanics, probability theory, or dynamical systems will be considered an asset, as well as proficiency in analytical and/or numerical methods. Enthusiasm for interdisciplinary research and collaboration across institutions is essential.
The PhD positions are fully funded, offering a competitive scholarship and access to excellent research facilities. Students will benefit from joint supervision between UNamur and UCLouvain, enabling them to build a strong, diverse skill.
Interested candidates are invited to submit a CV, a motivation letter, and contact information for two references. The review of applications will begin shortly and continue until the positions are filled. The successful candidates are expected to start their PhD in the fall of 2025.
Last update: 13/06/2025
Publications in connection with the EMOTIONS ARC research project
Carletti, T., Giambagli, L., Bianconi, G., Global Topological Synchronization on Simplicial and Cell Complexes, Physical Rev. Letters, (2023), 130, 187401. DOI: https://doi.org/10.1103/PhysRevLett.130.18740
J-F de Kemmeter, A. Byrne, A. Dunne, T. Carletti and M. Asllani, Emergence of power-law distributions in self-segregation reaction-diffusion processes, Phys. Rev. E, 110, (2024), pp. L012201. DOI: https://doi.org/10.1103/PhysRevE.110.L012201
Asllani, T. Carletti, F. Di Patti, D. Fanelli and F. Piazza, Hopping in the crowd to unveil network topology, Phys. Rev. Letters, 120, (2018), pp. 158301. DOI: https://doi.org/10.1103/PhysRevLett.120.158301
C. Hagendorf, and H. Rosengren, Nearest-neighbour correlation functions for the supersymmetric XYZ chain and Painlevé VI. Commun. Math. Phys. 405, 97 (2024). https://doi.org/10.1007/s00220-024-04977-w
J.-F. de Kemmeter, N. Robert and P. Ruelle, On λ-determinants and tiling problems, Journal of Physics A: Mathematical and Theoretical - Vol. 57, no. 1, p. 015209 (2024) https://doi.org/10.1088/1751-8121/ad0fb2
Ruelle, P., Double tangent method for two-periodic Aztec diamonds, Journal of Statistical Mechanics: Theory and Experiment- Vol. , no.12, p. 123103 (2022) https://doi.org/10.1088/1742-5468/aca4c4
Debin, J.-F. de Kemmeter and P. Ruelle, Fluctuations and arctic curve in the Aztec diamond, Belgian Journal of Physics- Vol. 1, no. 5, p. 18--26 (2022) http://hdl.handle.net/2078.1/275544
The involved partners
 |
|
 |
 |
EMOTIONS | A collaborative Research Action Project (ARC) - October 2024 - September 2029
Funded by the Federation Wallonie-Bruxelles (FWB), ARC projects are Concerted Research Action projects that aim at developing university or inter-university centres of excellence in fundamental research axes and, where possible, that carry out basic and applied research in an integrated manner and aim to make economic and social use of research results. They are awarded based on academic excellence of the applicants, the added value of each research group to achieve goals of research project, complementary skills of research teams and the methodology of proposed research program. They typically last for 4 to 5 years. In case of inter-university project, each team is financely supported by its own institution.
More information on the FWB website
